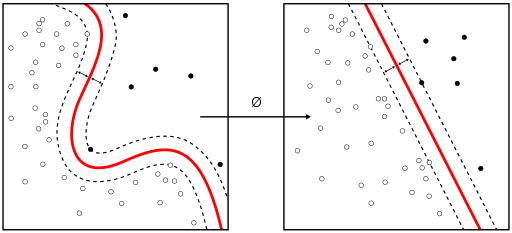
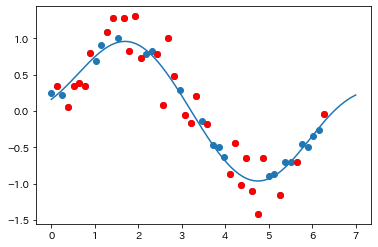
まとめ¶
今年度は、実践的なデータサイエンス、とくに機械学習の手法をデータの整理に生かすことを想定した内容にした。
データの「分類」(classification)と「回帰」(regression)が機械学習の2大テーマであるが、実験観測データの回帰分析がもっとも使う頻度が高いであろうと考え、それで筋を通した。
機械学習によるデータ処理の手法¶
最小2乗法と過学習の問題¶
- 線形単回帰
- 説明変数$x$と目的変数$y$の関係を$ y= w_0 + w_1 x$として、係数$w_0$, $w_1$を最小2乗法で推定
線形重回帰
- ボストンの住宅価格と各地点の特徴データをもとに、説明変数が多数ある場合(説明変数$\{x_1, x_2, \cdots , x_M\}$について
$$y = w_0 +w_1 x_1 + w_2 x_2 + \cdots + w_M x_M$$
なる関係があると想定して係数を推定
非線形回帰
- $x$と$y$が非線形な関係にある場合、べき級数近似
$$y = w_0 + w_1x + w_2x^2 + \cdots + w_M x^M$$
として係数を求める問題は説明変数を$\{x, x^2,\cdots , x^M\}$とすれば線形重回帰と同様である。
過学習
- 多項式近似では、$M$が大きい(データ数と同程度)の場合は、過学習がおきる。
加重減衰(正則化項)による過学習の回避¶
ridge回帰
$$ \tilde{E}({\bf w}) = \frac{1}{2} \sum_{n=1}^N \{y(x_n,{\bf w}) - t_n\}^2 + \frac{\lambda}{2}||{\bf w}||^2 $$
を最小にする$\{w_i,\ i=1,\cdots, M\}$を求める。
- Lasso回帰
非線形関係を表す様々なフィッティング関数¶
べき多項式以外のフィッティングへの一般化
非線形な関係のフィッテングは、$\{\phi_1(x) + \phi_2(x) + \cdots + \phi_M(x)\}$を適当に選び
$$ y(x, {\bf w}) = w_1 \phi_1(x) + w_2 \phi_2(x) + \cdots + w_M \phi_M(x) $$のように一般化できる。
特に、区間$[a,b]$の間のフィッティングを、区間を$M+1$個で割り、そこをピークするガウス関数
$$ \phi_i (x) = \exp \left( - \frac{(x - \mu_i)^2}{2\sigma^2}\right),\quad \mu_i = \frac{b-a}{M}i,\quad i=1,2,\cdots M $$を使うことが多い。これをガウス基底と呼ぶ。
ベイズ統計回帰モデル¶
パラメータの事前分布を仮定し、データが追加されるごとに逐次学習してパラメータの確率分布をベイズの定理に従って計算する手法。
(PRMLの図1.16):
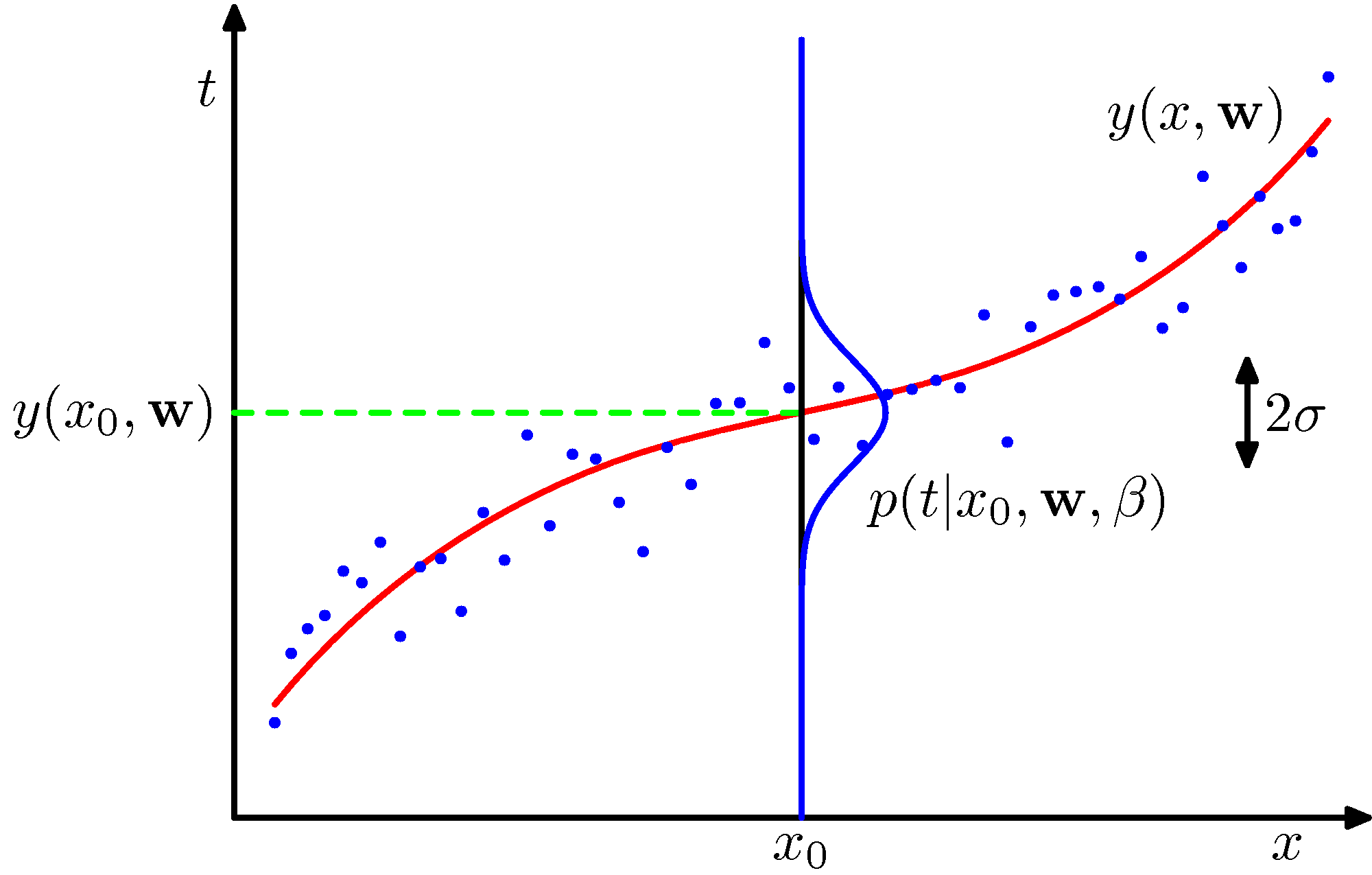
- 最適なパラメータ値だけではなく、パラメータの確率分布を得ることができる
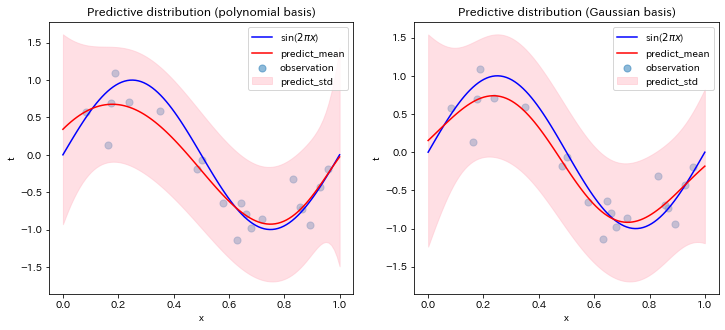
カーネル法¶
ガウシアン基底を用いたベイズ統計回帰モデルの表式から、学習は、基底関数$\phi$の前の係数の確率分布ではなく、基底関数と係数をカーネル関数という形にまとめられることをみた。
$$ y(\boldsymbol{x}_i)=\sum_{k=1} w_k \phi_k (\boldsymbol{x}_i) +b $$例えば、RBF(ガウシアン)カーネル
$$ k(\boldsymbol{x},\boldsymbol{x'}) = \exp ( -\gamma ||\boldsymbol{x}- \boldsymbol{x'}||^2) $$その他の機械学習手法による回帰問題へのアプローチ¶
ニューラルネット(パーセプトロン)
決定木のアンサンブル学習(ランダムフォレスト)
skit-learnに含まれる機械学習法の共通事項¶
データの正規化(reguralization)
- 複数の説明変数があるとき、各変数の値の平均値と分散を統一規格(平均、分散とも1)にすることにより、重要度の軽重を比較できるようにする。
- scikitlearnでは、
from sklearn.preprocessing import StandardScaler
ハイパーパラメータの最適値探索
scikitlearnのGridSearchの利用
import sklearn.model_selection as ms est = ms.GridSearchCV(svm.LinearSVC(), {'C': np.logspace(-3., 3., 10)})
自然科学とデータサイエンス¶
自然科学(Natural Science)
- a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe.
- 「観察事実に拠りどころを求めつつ法則を追及すること」(「物理学とは何だろうか」朝永振一郎、岩波新書)
- The scientific method seeks to explain the events of nature in a reproducible way
- 「真の物理法則というものは、常に、一枚のハガキに書けるようなものである」 (Schrödingerの言葉と伝えられるが出典はわからない。)
⇒ 原理に基づくモデリングと数値実験(Numerical Simulation)
- データサイエンス(Data Science)
- 必ずしも「法則」を探求するものではない。
- 意思決定のため(Data-driven decision)、人間の目や耳の代わり(識別)とか
- 説明変数と目的変数の関係をデータから推定
- 背後にシンプルな自然法則があるわけではない対象もあり得る
- 人間個人あるいは集団の行動の結果として現れる社会現象など
- 生物・医学・生態学などの分野の事象
- 画像認識 ...
- したがって、関係は明確になっても、それをよく知られた関数として表せない手法も多い。逆にその方が的確に短時間で予測機械を作ることができる。
- 必ずしも「法則」を探求するものではない。
通底するのは数学 (その意味で、数学は自然科学の範疇には入らない)
とはいえ、創薬、大規模加速器実験などなど自然科学ベースの対象物の探索にも用いられるようになり、一言では言い表せない状況も出現している。