前章では，
物体に仕事がなされたとき，仕事の合計が物体の運動エネルギーに加わる
ことを学んだ．
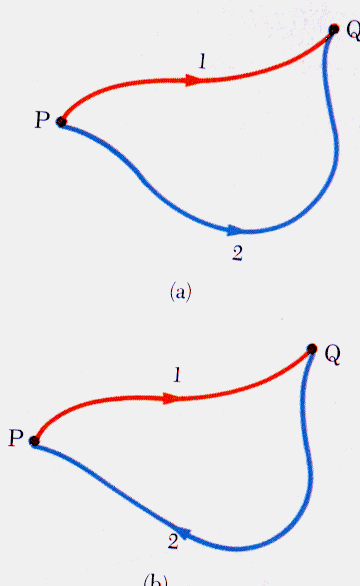
物体に力を加えて移動させるとき，仕事量が始点と終点だけによって決まる（経路によらない）とき，その力を 保存力 とよぶ．
重力，摩擦力のように力学の授業でよく登場するものは保存力である．
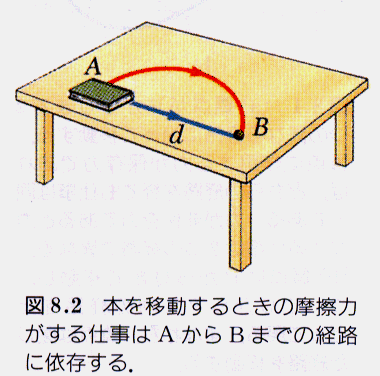
摩擦が関係する力は非保存力である．
現時点では，「摩擦」以外の力はほとんど保存力であると思って良い．
摩擦力は運動エネルギーを減じるようにはたらく．この分は熱エネルギー（分子の乱雑な運動エネルギー）に変化する．そのことをエネルギーの 散逸 (dissipation)とよぶ．
この節以降は 保存力についてだけ 扱う．
力の積分に負符号をつけたものをポテンシャルエネルギーと呼ぶ
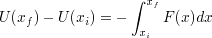
ニュートンの運動方程式
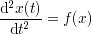
を積分（左辺については，テキストp170参照：授業で説明)すると
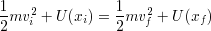
がなりたつ．つまり，
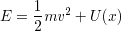
は一定に保たれる．これを 力学的エネルギー と呼ぶ．
質量mの物体にはたらく力は，地上付近では一定値 mg であるから，鉛直上向き方向にy軸をとると，
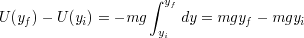
となる．
落下は，運動エネルギーが増し，ポテンシャルエネルギーが減る過程である．
エネルギー的考察が有用である例として例題８．４を考えてみよう．
力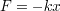 
の積分（ポテンシャルエネルギー）は
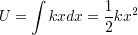
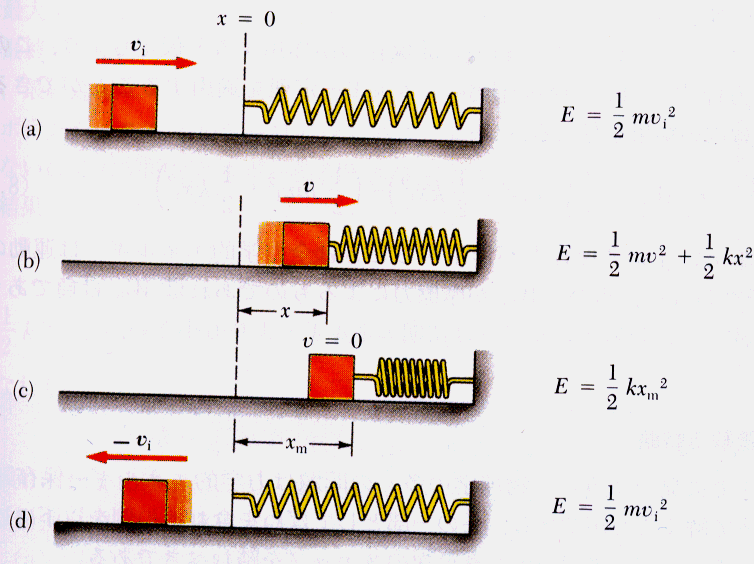
であるから，この場合の物体の力学的エネルギーは
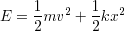
と書かれる．
例題８．６を考えてみよう．
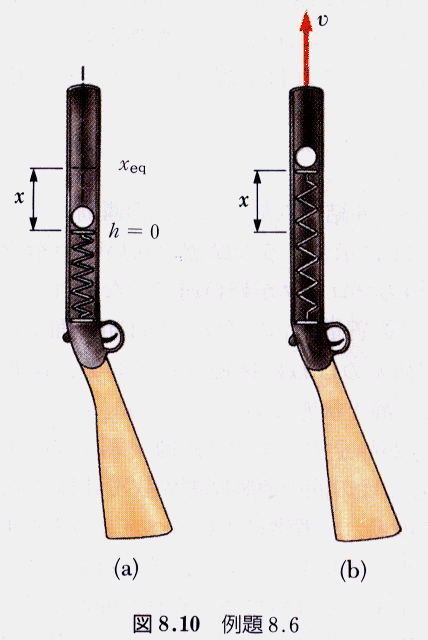
保存力を積分するとポテンシャルエネルギーの表式が得られた．逆にポテンシャルエネルギーを微分すると力になる．
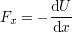
一次元での問題では，FあるいはUが位置xだけの関数であるとき，力は保存力であるといえる．
最後にp.208の「まとめ」で復習しておこう．
2,3,4,10,29,43
斜面を滑る物体のエネルギー保存則に関わるシミュレーションとして，Webブラウザで見られるものを紹介する． 次のページの Dynamics -> Coservation of Energy を閲覧してみてほしい．