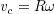
この章の目標は
の2点とする.
球や円筒が面上をころがる運動を理解しよう.
図のように転がりは,重心が面と平行に移動することと,回転運動の両方をまとめて扱わなければならないことにポイントがある.しかし,それはシンプルな結論になる.
まず,11.2図をみながら,回転角速度と重心の平行移動速度の間に
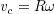
の関係があること.両辺を微分することにより加速度についても
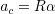
の関係があることを理解しよう.
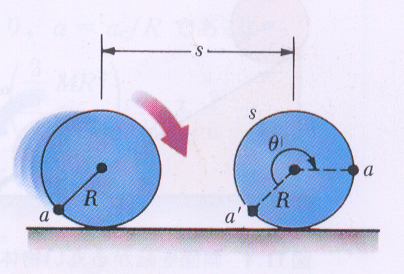
瞬間的な回転は,接地点を中心に起っている.そのときの全運動エネルギーは接地点を中心とする回転運動エネルギーに等しい:
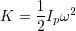

前節の授業ではとばしたが,点Pを中心とする慣性モーメントと重心Cを中心とする慣性モーメントの間には「平行線定理」
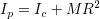
が成り立つ.これを代入すると
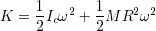
となる.ここで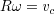 あること使えば,
あること使えば,
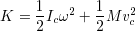
が得られる.第1項は重心回りの回転エネルギーを表し、第2項は重心に質量が集中していると見なしたときの運動エネルギー(並進の運動エネルギー)を表す.このように並進運動と回転運動のエネルギーの単純な和で表せるのである.
以上のことを,斜面を転がる物体に適用して(11.6)式を導き,この式から章末の「質問1 5」を考えてみよう.
ベクトル積の定義の(11.13)式(p.287)にしたがって理解する.
2つのベクトル A , B に対して, A の方向にx軸をとり, B をx-y平面内にとり
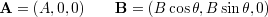
定義にしたがって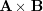 を成分ごとに求めてみると
を成分ごとに求めてみると
となることがわかる.つまり外積は, A , B に対して垂直な方向(z軸)であり,大きさは,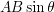 である.((11.9)式)
である.((11.9)式)
分配則(11.11),微分(11.12)も確認しておこう.
回転に角加速度を与えるのは中心から対象物(剛体の部分)に対するベクトル(動径)に対して垂直方向(回転円の接線方向)の力である((10.7節). ふつう用いている右手系で考え,方向を加味すると,ベクトル積を用いてトルクは(11.7)のように定義できる.
角運動量保存則の例として,猫の落下についてこのページに分かりやすい図があるので,参照しながら考えてみよう.
無重力状態での動きもおもしろいですね. (5:30くらいからの映像をみてみてください.映像はこのページから教えてもらいました.)