決定木法メモ

「樹木構造接近法」（下川敏雄ら、共立出版）による

CART(Classification and Regression Trees)法

データ集合を$\mathcal{L} = \{y_n, \boldsymbol{x}_{n}\}$ $(n=1,\cdots,N)$とする。

木(tree)の成長過程

最初は一つのノード（root)にすべてのデータがあるとして、それらをポリシーにより枝分かれさせていく。

あるノード(節)を子ノードに分けるポリシーは、ノード内の不均一性測度を小さくすることである。 あるノード$t$の回帰残差を $$ r_{reg}(t) = \frac{1}{N(t)}\sum_{n\in t} \{y_n - \bar{y}(t)\},\quad \bar{y}(t)=\frac{1}{N(t)}\sum_{n\in t} y_n $$ を用いて、不均一性測度は、 $$ R(t) = pr(t)r_{reg}(t), \quad pr(t) = N(t)/N $$ で定義する。

以上は回帰木の場合である。

分類木の場合

応答$y_n$は$K$個のクラスのいずれかの値をとる「分類木」について考える。

ノード$t$において応答（値）が$k$をとる確率は $$ pr(k|t) = \sum_{n\in t} \mathbb{1} (y_n = k)/ N(t) $$ である。ここで$\mathbb{1}(\cdot)$はカッコ内が真なら1, 偽なら0を撮る関数である。$t$における予測値は、その木にもっとも多い応答の数として次のように定義する（多数決）。 $$ \newcommand{\argmax}{\mathop{\rm arg~max}\limits} \hat{k}(t) = \argmax_{k} pr(k|t) $$

この場合は、ノード$t$の不均一性測度として次のものが考えられる

  • 誤分類率（期待値に一致しない確率）： $r_{c1}(t) = 1 - pr(\hat{k}(t)| t)$
  • Gini係数： $r_{c2}(t) = \sum_{k\neq k'} pr(k|t) pr(k'|t) = \sum_{1\le k \le k'} pr(k|t) (1- pr(k|t))$
  • エントロピー基準： $r_{c3} = -\sum_{1\le k\le K} pr(k|t)\log pr(k|t)$

$t$を$t_L$と$t_R$に分岐させる規則を式で表すと $$ s_t^* = \argmax_{s_t\in S_t} \Delta R(s_t, t),\quad \Delta R(s_t,t) = R(t) -R_L (t_L) - R_R(t_R) $$ と表される。要は、不均一性測度が最大になるように分類するということである。

木の刈り込み過程

木を成長させていけば、$R$は減少していく。最後は１つのノードに一つのデータだけになることになってしまう。それはやりすぎである。そこで木が大きくなりすぎないように複雑度のペナルティを加え、それが最小にすることを考える。

木のノード集合$T$のうち、末端のノード（葉）の集合を$\tilde{T}$とし、その個数を$|\tilde{T}|$で表す。複雑性コストを加えた量 $$ R_{\alpha}(T) = R(T) + \alpha |\tilde{T}| $$ を最小にする木をみつける。

最適な木の決定

この説の記述は省略が多く、わかりにくいが、全体としては、データの一部分を学習データ、残りをテストデータとして、交差検定を行って最適な木をみつけるポリシーが書かれていると思う。

CARTの利用例

住宅価格データBoston使う。（パッケージ MASSに含まれている。）

持ち家価格の中央値(medv)をその他の量を説明変数として、影響を与える要因を分析する。

  • CART法は、パッケージrpartに入っている
  • "medv ~ ."はmedvが目的変数、それ以外を説明変数とするという意味
  • 目的変数(応答)が連続的な値の場合は回帰木(anova)を、因子型であれば分類木(class)を利用。
In [1]:
data(Boston, package = "MASS")
names(Boston)
  1. 'crim'
  2. 'zn'
  3. 'indus'
  4. 'chas'
  5. 'nox'
  6. 'rm'
  7. 'age'
  8. 'dis'
  9. 'rad'
  10. 'tax'
  11. 'ptratio'
  12. 'black'
  13. 'lstat'
  14. 'medv'
In [3]:
library(rpart)
rtree0<-rpart(medv~., data=Boston, method="anova", control=rpart.control(cp=0))
plot(rtree0, uniform=TRUE, margin=0.1)
text(rtree0, cex=0.6)

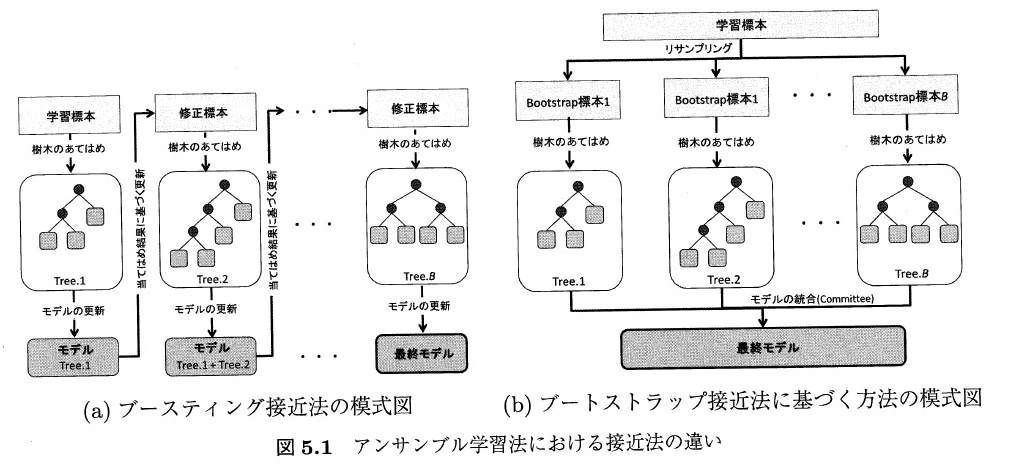
アンサンブル学習法

アンサンブル学習法は、開会学習あるいはデータ・マイニングの分野では、集団学習(Committee Machine)と呼ばれている。

方法はおもに2つに分類される。

  • ブースティング接近法 モデルへの木の追加過程において、予測誤差を逐次改善する方法
  • ブートストラップ接近法 ブートストラップ標本に対して、あてはめた個々の基本学習機の平均値（回帰問題の場合）、あるいは多数決（分類問題）よりモデルが得られる。

「樹木構造接近法」図５．１

boosting_bootstrap

In [ ]: